前言:Derivative 詞義廣泛,理解中文語境下的多元面貌

在現代知識體系中,「derivative」這個詞彙如同一條隱形的線索,串聯起數學、金融、語言學甚至文化創作等多個領域。它不僅僅是一個外來語彙,更是一種思維方式的體現——從某個基礎出發,衍生出新的形態與價值。然而正因其應用範圍極廣,不同專業背景的人對它的理解往往南轅北轍。有人想到的是函數圖形上的切線斜率,有人則聯想到高風險高報酬的金融交易工具,也有人僅將其視為語言中由詞根變化而來的新詞。這種語意的多義性,常讓初學者陷入混淆。
本文旨在打破領域界限,以整合性的視角深入剖析「derivative」在各個層面的核心含義。無論你是正在學習微積分的學生、關注市場動態的投資人,還是對語言演變感興趣的文史愛好者,都能從中獲得清晰且具體的指引。透過系統性的解構與實例說明,我們將幫助你建立對這個關鍵概念的完整認知架構,不再因術語差異而產生誤解。
Derivative 的基本中文翻譯與詞性解析
要真正掌握「derivative」一詞,首先必須理解其在中文語境中的多種翻譯方式,並釐清其詞性所帶來的語意差異。這個詞根據使用場景與文法功能,可靈活轉化為不同的中文對應詞,若僅依字面直譯,極易產生誤解。
- 名詞 (N.):
- 衍生物;派生詞: 泛指從原有事物延伸或演變而來的新形態。在語言學中,這類詞彙通常透過添加詞綴形成,例如「教師」是從「教」這個動詞派生而來的名詞。
- 導數: 數學領域中最精確的用法,專指函數在某一點的瞬時變化率,為微積分學的核心概念之一。
- 衍生性金融商品: 金融市場中常見的術語,指價值取決於其他資產表現的合約型商品,如期貨、選擇權等。
- 形容詞 (Adj.):
- 派生的;衍生的;借鑒的: 用以描述某事物並非原創,而是基於既有成果進一步發展而成。例如一篇研究論文若大量引用他人理論而缺乏創新,可能被評為過於「衍生性」。
值得注意的是,同一個英文單字在不同領域承載截然不同的專業內涵,但背後共通的精神皆圍繞著「源自某處」、「由某物引出」這一核心理念。掌握此一脈絡,有助於在跨領域溝通時避免誤讀。
數學領域的 Derivative:微積分中的「導數」
在數學體系中,「derivative」最精確且不可替代的中文翻譯便是「導數」。它是微積分學的基石之一,提供了一種精確描述變化的工具。從物理運動到經濟模型,幾乎所有涉及「速率」或「趨勢」的問題,都離不開導數的應用。
什麼是導數?從變化率到極限概念
導數的本質,在於衡量一個函數在某一瞬間的變化快慢。舉個生活化的例子:當你開車時,車速表顯示的數字就是你所在位置的「瞬時速度」,這正是位移對時間的導數。換句話說,它告訴我們「此刻正在以多快的速度前進」,而非一段路程的平均速度。
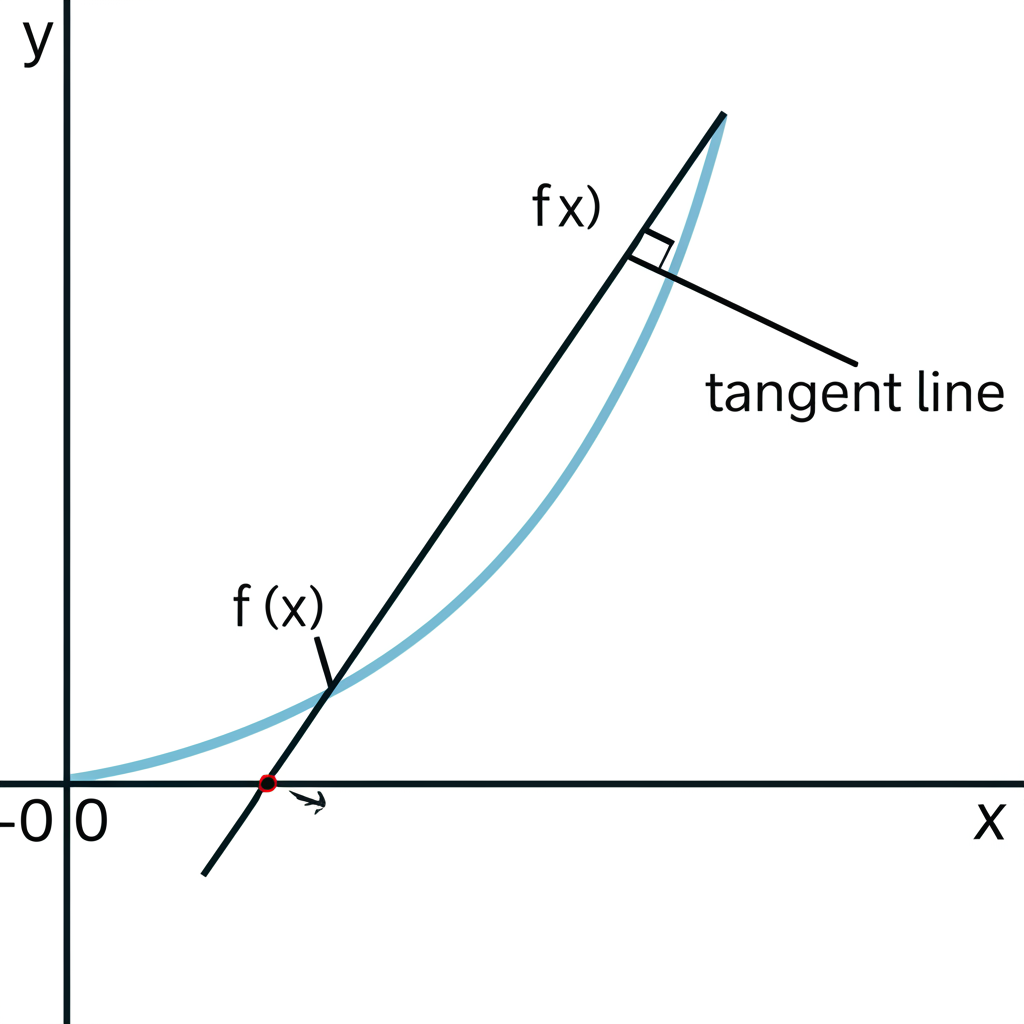
在幾何上,導數則體現為函數曲線在某一點的切線斜率。想像你在一座起伏的山路上駕駛,導數就像是你所在位置道路的陡峭程度——往上爬是正斜率,下坡是負斜率,平緩處則接近零。
其數學定義建立在極限的思想之上:對於一個函數 \(f(x)\),它在點 \(x_0\) 的導數 \(f'(x_0)\) 定義為:
\[ f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) – f(x_0)}{h} \]
這個公式背後的邏輯是,先計算從 \(x_0\) 到 \(x_0 + h\) 之間的平均變化率(即割線斜率),再讓 \(h\) 趨近於零,使這個區間無限縮小,最終得到該點的瞬時變化率。這個過程如同將望遠鏡對準函數曲線的某一點,逐步放大,直到曲線看起來像一條直線——那條直線就是切線,其斜率即為導數。欲更深入了解導數的幾何詮釋,可參考 維基百科對導數的詳細解釋。
導數的基本運算規則
面對實際問題時,我們不可能每次都回到極限定義去求導數。因此,數學家發展出一套高效且系統化的運算規則,讓複雜函數的導數計算變得可行。以下是常見的基本法則:
- 常數法則: 若 \(c\) 為常數,則 \(\frac{d}{dx}(c) = 0\)。這表示固定不變的量,其變化率自然為零。
- 冪次法則: 若 \(n\) 為任意實數,則 \(\frac{d}{dx}(x^n) = nx^{n-1}\)。這是多項式函數求導的基礎,例如 \(x^3\) 的導數為 \(3x^2\)。
- 常數倍數法則: 若 \(c\) 為常數,則 \(\frac{d}{dx}(cf(x)) = c \frac{d}{dx}(f(x))\)。係數可以直接提出來。
- 和差法則: \(\frac{d}{dx}(f(x) \pm g(x)) = \frac{d}{dx}(f(x)) \pm \frac{d}{dx}(g(x))\)。函數加減的導數等於各自導數的加減。
- 積法則: \(\frac{d}{dx}(f(x)g(x)) = f'(x)g(x) + f(x)g'(x)\)。兩個函數相乘時,導數需考慮雙方的貢獻。
- 商法則: \(\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) – f(x)g'(x)}{[g(x)]^2}\),其中 \(g(x) \neq 0\)。適用於分式結構的函數。
- 鏈鎖法則: \(\frac{d}{dx}(f(g(x))) = f'(g(x))g'(x)\)。這是處理合成函數的關鍵,例如對 \(\sin(x^2)\) 求導時不可或缺。
這些規則構成了微分運算的骨架,熟練運用它們,才能順利處理現實世界中的複雜模型。
導數的應用:從函數分析到實際問題
導數的價值不僅體現在理論推導,更廣泛應用於各類實際情境:
- 函數分析:
- 尋找極值: 當函數達到局部最大或最小值時,其導數通常為零(或不存在)。這被稱為臨界點,是優化問題的關鍵切入點。
- 判斷增減性: 導數的正負直接反映函數的上升或下降趨勢。若在某區間內 \(f'(x) > 0\),則函數遞增;反之則遞減。
- 判斷凹凸性: 二階導數(即導數的導數)可用來判斷曲線是向上彎(凹)還是向下彎(凸),進一步輔助繪圖與分析。
- 實際問題:
- 優化問題: 舉例來說,一家製造商希望在成本與產量之間取得平衡,使利潤最大化。透過建立利潤函數並對其求導,可精確找出最佳生產規模。
- 物理學: 在運動學中,位移對時間的導數是速度,速度對時間的導數則是加速度。這套框架成為牛頓力學的數學基礎。
- 經濟學: 邊際成本、邊際收益等概念皆以導數定義,幫助企業決策者評估每多生產一單位產品的效益與成本。
金融領域的 Derivative:解析「衍生性金融商品」
在金融市場中,「derivative」指的是一類特殊金融工具——「衍生性金融商品」,又稱「金融衍生品」。這些商品本身不具獨立價值,而是與某種基礎資產掛鉤,其價格波動直接反映後者的市場表現。
什麼是衍生性金融商品?核心概念與特徵
衍生性金融商品的價值來源於「標的資產」(Underlying Assets),這些資產可能是股票、債券、外匯、利率、商品(如原油、黃金)、指數,甚至是天氣或信用事件。買賣雙方根據對未來價格走勢的預期,簽訂合約,約定在未來某個時間點以特定條件進行交易。
這類商品之所以受到機構與投資人青睞,主要因其具備以下特質:
- 槓桿效應: 投資人只需投入少量資金(如保證金或權利金),就能參與大額資產的價格變動,放大潛在報酬,但也同步放大損失風險。
- 契約性質: 衍生品本質上是法律合約,明確規範交易時間、價格、數量等條件,具有高度的彈性與可定制性。
- 風險管理功能: 企業可用來對沖價格波動風險,例如農場主透過期貨合約鎖定未來銷售價格,避免收成時市價下跌。
進一步了解此類商品的市場機制與風險特性,可參考 Investopedia 對金融衍生品的解釋。
主要衍生性金融商品類型
市場上常見的衍生性金融商品可歸納為四大類,各自適用於不同目的與交易環境:
- 期貨 (Futures):
一種標準化的遠期合約,在交易所集中交易,買賣雙方均有義務於到期日以約定價格交割資產。由於每日結算與中央擔保機制,信用風險較低,流動性高,廣泛用於商品與金融指數交易。
- 選擇權 (Options):
賦予買方在特定時間內,以履約價買入(買權)或賣出(賣權)標的資產的權利,但無需強制執行。賣方則須在買方行使權利時履行義務。這種「權利與義務不對等」的特性,使其成為風險可控的投資與避險工具。
- 遠期契約 (Forwards):
與期貨類似,但屬於非標準化、個別協商的合約,通常在店頭市場(OTC)進行。由於缺乏中央清算,交易雙方直接承擔彼此的信用風險,適合有特定需求的機構用戶。
- 掉期 (Swaps):
雙方約定在未來一段期間內交換現金流的合約。最常見的是利率掉期(固定利率與浮動利率交換)與貨幣掉期(不同幣別的本金與利息交換),廣泛應用於企業財務結構調整與風險管理。
下表簡要比較了這些主要衍生性金融商品的特性:
| 特性 | 期貨 (Futures) | 選擇權 (Options) | 遠期契約 (Forwards) | 掉期 (Swaps) |
|---|---|---|---|---|
| 標準化程度 | 高 | 高 | 低 (客製化) | 低 (客製化) |
| 交易場所 | 交易所 | 交易所/OTC | OTC | OTC |
| 義務/權利 | 有義務 | 有權利無義務 (買方) | 有義務 | 有義務 |
| 信用風險 | 低 (交易所擔保) | 相對低 (買方), 高 (賣方) | 高 | 高 |
衍生性金融商品的功能與風險
衍生性商品在現代金融體系中扮演多重角色,但其複雜性也伴隨高度風險:
- 功能:
- 避險 (Hedging): 實體企業或投資人利用衍生品抵消價格波動風險。例如航空公司購買燃油期貨,以穩定營運成本。
- 投機 (Speculation): 投資者運用槓桿押注市場走勢,期待從價格變動中獲利。此行為雖提升市場流動性,但若判斷錯誤,虧損可能遠超本金。
- 套利 (Arbitrage): 當同一資產在不同市場出現價差時,套利者同時買賣以鎖定無風險利潤,有助於市場價格回歸合理水平。
- 風險:
- 市場風險: 標的資產價格劇烈波動可能導致衍生品價值急挫。
- 信用風險: 在OTC市場,若交易對手違約,將面臨損失。
- 流動性風險: 某些冷門合約可能難以脫手,尤其在市場動盪時。
- 操作風險: 包含系統故障、人為疏失或詐欺等內部管理問題。
- 法律風險: 合約條款模糊或當地法規變動,可能影響執行效力。
正因為其雙面刃特性,參與衍生品市場需具備扎實的知識基礎與嚴謹的風險控管策略,絕非一般散戶可輕易涉足的領域。
Derivative 與 Derivation:常見混淆與區分
「Derivative」與「Derivation」發音相近,拼寫相似,常被誤用或混為一談。然而,兩者在語意上存在根本差異,正確區分有助於提升專業表達的精準度。
- Derivative (衍生物、導數、衍生性金融商品):
指的是**結果或最終產出**。它是一個名詞,代表從某個基礎發展而來的具體存在。
- 數學中: 經過微分運算後得到的函數,稱為原函數的「導數」,也就是「derivative」。
- 語言學中: 像「reader」是由「read」加上後綴「-er」所形成的「派生詞」,這就是一種語言上的 derivative。
- Derivation (派生、推導、起源):
指的是**過程或產生的方式**。它強調的是從起點到終點的演變路徑。
- 數學中: 從原始函數一步步應用法則求出導數的過程,稱為「derivation」。例如「我們透過鏈鎖法則完成這個函數的推導」。
- 語言學中: 分析一個詞是如何由詞根與詞綴組合而成的過程,稱為「詞彙派生 (word derivation)」;而一個詞的歷史來源,則稱為「語源 (etymological derivation)」。
簡單來說,derivation 是過程,derivative 是結果。例如,你不會說「這個詞的 derivative 是什麼」,而應該問「這個詞的 derivation 是什麼」,因為你想了解的是它的形成過程。Merriam-Webster 字典對 “derivation” 的定義也明確指出其涵義為「源頭」或「形成行為」。
Derivative 的發音與詞源簡介
「Derivative」的英文發音為 /dɪˈrɪvətɪv/,近似「迪-瑞-瓦-提夫」。重音落在第二音節,是學習者需留意的發音細節。
這個詞的根源可追溯至拉丁文「derivare」,原意為「引導水流離開主河道」或「從源頭引出」。其中「de-」表示「從…」,「rivus」意為「溪流」,合起來就是「引流」的概念。隨著時間演進,這項意象從物理性的水流,擴展為抽象意義上的「從某事物中引申、推導」。中古英語時期,該詞進入英語體系,逐漸發展出數學、金融與語言學等多方面的用法,但其核心精神始終未變:強調「源出」與「依賴」的關係。這種從具體到抽象的語義演變,正是語言生命力的展現。
結論:掌握 Derivative,打開知識新視野
「Derivative」雖僅為一字,卻承載跨越學科的深遠意涵。無論是在數學中作為分析變化的利器,金融市場中作為風險管理與資本配置的工具,還是語言學中作為詞彙生成的機制,它都展現了人類如何從基礎元素創造出更複雜結構的智慧。理解這個詞的多重面貌,不只是掌握術語翻譯,更是培養跨領域思維的重要一步。
在資訊快速流動的當代,能精準解讀專業語境中的關鍵字,往往決定溝通的效率與深度。透過本文的系統性梳理,希望能幫助你擺脫片段式理解,建立起對「derivative」的整體認知框架。未來無論面對微積分習題、財經新聞,或是語言學討論,都能從容應對,並進一步延伸探索相關知識脈絡。
常見問題 (FAQ)
Derivative 在中文裡有哪些主要的意義?
Derivative 在中文裡主要有三大意義:
- 數學: 指「導數」,表示函數的瞬時變化率。
- 金融: 指「衍生性金融商品」,其價值依賴於其他基礎資產。
- 一般詞彙/語言學: 指「衍生物」或「派生詞」,表示從其他事物發展或引申而來的東西。
微積分中的「導數」是什麼意思,它有什麼實際用途?
微積分中的「導數」是衡量函數在某一點瞬時变化率的工具。它在幾何上代表函數曲線在該點的切線斜率,在物理上代表瞬時速度或加速度。
實際用途包括:
- 優化問題: 尋找最大利潤、最小成本或最佳效率。
- 函數分析: 判斷函數的增減、極值和凹凸性。
- 物理學: 計算瞬時速度、加速度等動態變化。
什麼是「衍生性金融商品」?它與一般金融商品有何不同?
「衍生性金融商品」是一種金融合約,其價值源自於其他基礎資產(如股票、債券、利率、商品等)。
它與一般金融商品的主要不同在於:
- 價值來源: 衍生品價值不獨立,依賴於標的資產;一般金融商品(如股票、債券)有其內在價值。
- 槓桿效應: 衍生品通常具有較高槓桿,能以小博大;一般金融商品槓桿較低。
- 契約性質: 衍生品是買賣雙方在未來交易的合約;一般金融商品是現貨交易或所有權憑證。
「期貨」、「選擇權」、「遠期契約」和「掉期」這些常見的衍生性金融商品之間有什麼區別?
這些衍生性商品的主要區別在於其標準化程度、交易場所、以及買賣雙方的權利與義務:
- 期貨 (Futures): 標準化合約,交易所交易,買賣雙方都有義務在未來履約。
- 選擇權 (Options): 賦予買方權利而非義務,賣方有義務;可在交易所或OTC交易。
- 遠期契約 (Forwards): 客製化合約,OTC交易,買賣雙方都有義務履約,信用風險較高。
- 掉期 (Swaps): 客製化合約,OTC交易,雙方同意交換一系列現金流(如利率或貨幣)。
投資衍生性金融商品有哪些潛在風險?
投資衍生性金融商品伴隨多種潛在風險:
- 市場風險: 標的資產價格波動導致的損失。
- 信用風險: 交易對手不履約的風險,尤其在OTC市場。
- 流動性風險: 無法迅速以合理價格買賣合約的風險。
- 槓桿風險: 高槓桿可能放大收益,但也可能導致巨額虧損。
- 操作風險: 因系統、流程或人員失誤導致的風險。
「Derivative」和「Derivation」這兩個詞在意義上有何不同?
「Derivative」通常指結果或產物,例如數學中的「導數」或金融中的「衍生品」。
而「Derivation」則指過程或推導的行為,例如數學中「求導數的過程」或語言學中「詞彙的派生過程」。簡而言之,derivation 是過程,derivative 是過程的結果。
除了數學和金融,Derivative 在其他領域還有什麼含義?
除了數學和金融,Derivative 在其他領域也有應用,例如:
- 語言學: 指「派生詞」,從其他詞根或詞綴組合成的新詞。
- 化學: 指「衍生物」,從某種化學物質衍生出來的化合物。
- 藝術/文化: 指「派生作品」或「模仿作品」,從原作中汲取靈感或改編而來的作品。
學習 Derivative 相關知識對日常生活或職業發展有幫助嗎?
是的,學習 Derivative 相關知識非常有幫助:
- 日常生活: 提升邏輯思維和分析能力,理解各種變化率的概念。
- 職業發展:
- 金融業: 投資銀行、基金管理、風險管理等都需要深入理解衍生品。
- 工程/科學: 微積分是許多工程和科學領域的基礎工具。
- 數據分析: 理解變化趨勢和模型優化。
Derivative 的英文發音是什麼?
Derivative 的英文發音為 /dɪˈrɪvətɪv/,近似中文發音「迪-瑞-瓦-提夫」。
金融衍生品的主要功能是避險還是投機?
金融衍生品同時具有避險和投機兩大主要功能,具體取決於使用者的意圖和策略。
- 避險: 企業和投資者利用衍生品來管理和降低基礎資產價格波動帶來的風險。
- 投機: 投資者利用衍生品的高槓桿特性,預測市場走向以期獲取高額利潤。
- 此外,它還可用於套利,利用市場上的價格不平衡來獲取無風險收益。